CS 371: Module 9: Exercise 0 (1.5 Points)

Module content by Professor Tralie. Module autograder developed by Professor Tralie and Professor Mongan.

---

Exercise Goals

The goals of this exercise are:

1. To apply recursive calls that track depth to reach a stopping condition

Fill in the code below to draw the Sierpinski triangle up to a specified MAX_DEPTH of recursion. If you are not at the max recursion, you will need to make a few recursive calls. The image below should help you to figure out which coordinates to draw in each recursive call. Be sure to add one to the depth parameter on each recursive call to avoid infinite recursion!

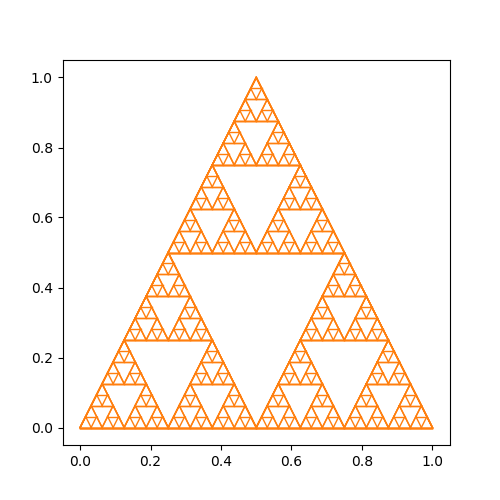
If this worked properly, you should see the following image

Enter your Ursinus netid before clicking run. This is not your ID number or your email. For example, my netid is ctralie (non Ursinus students can simply enter their name to get this to run, but they won't get an e-mail record or any form of credit)

Netid

Clicking Run below will check your work and, if it passes, will submit your work automatically. You must be connected to the VPN for submission to be successful! You will receive a copy of your code via e-mail, so you'll know that it was submitted if you receive that e-mail! VPN access requires Multi-Factor Authentication, which sends you a code when you log into the network. Instructions on configuring these for your account can be found here.

import io, base64 img_str = "" def save_figure_js(): global img_str buf = io.BytesIO() plt.savefig(buf, format='png') buf.seek(0) img_str = "data:image/png;base64,{}".format(base64.b64encode(buf.read()).decode('UTF-8'))

Imports / Setup

import numpy as np import matplotlib.pyplot as plt MAX_DEPTH = 6 def draw_triangle(x0, y0, x1, y1, x2, y2, c="C1", linewidth=1): """ Draw a triangle at the specified coordinates Parameters ---------- x0, y0, x1, y1, x2, y2: Coordinates of points c: string Color linewidth: float linewidth of line to draw """ plt.plot([x0, x1], [y0, y1], c, linewidth=linewidth) plt.plot([x1, x2], [y1, y2], c, linewidth=linewidth) plt.plot([x2, x0], [y2, y0], c, linewidth=linewidth)

Student Code

def draw_sierpinski(x0, y0, x1, y1, x2, y2, depth=0): """ Draw a sierpinski triangle at the specified coordinates Parameters ---------- x0, y0, x1, y1, x2, y2: Coordinates of points depth: int Depth of the recursion linewidth: float linewidth of line to draw depth: int Depth of recursion """ if depth < MAX_DEPTH: draw_triangle(x0, y0, x1, y1, x2, y2) ax = (x0+x2)/2 bx = (x1+x2)/2 cx = (x0+x1)/2 ay = (y0+y2)/2 by = (y1+y2)/2 cy = (y0+y1)/2 ## TODO: Do recursive calls to draw_sierpinski

Test Code Block

plt.figure(figsize=(5, 5), dpi=100) draw_sierpinski(0, 0, 1, 0, 0.5, 1) save_figure_js()

Output

Figure