Background

As we saw in module 8, a hash table or symbol table is an efficient way to address the "needle in a haystack problem" where we want to find an object efficiently in a large set of objects.

In implementation, a hash table consists of an array of linked lists. Each linked list is referred to as a bin, and its index in the list is referred to as the bin index. The "hash code" of an object under search tells us which bin index to visit to find it. In practice, we need to fix n bins, so we take the bin index as hash_code % n. For example, if we had the following hash codes which had a range from 0 to 11 below:

but then we fixed the number of bins at n = 7, we'd have the following hash table

There is a clear space-time tradeoff with the design of hash tables. If we use more bins, then the number of collisions (objects sharing the same bin) goes down, but we may also have empty bins. Conversely, using too few bins leads towards a large number of collisions, but no bins are wasted. Thus, we seek to analyze the time complexity of searching for objects under a hash table as we vary the number of bins and the total number of objects that are in the hash table.

Of course, we can put all of our objects into a linked list, which will take worst case O(N) time. We can also put them into a sorted list, which takes worst case O(log(N)) time using binary search. But as it turns out, we can do even better with hash maps. Intuitively, narrowing down our search to a single bin is extremely helpful, though it will be a little more difficult to show theoretically. In this class exercise, we will do some experiments to get a handle on this analysis

Balls/Bins Model

Often when we mathematically analyze things, it's helpful to "abstract away" our problem to a more concise problem that retains what we're trying to analyze. In the case of hash tables, let's think about throwing m balls (which represent our objects) into n bins (which represent our hash table bins) randomly. Below is an example of this with m = 100, n = 10:

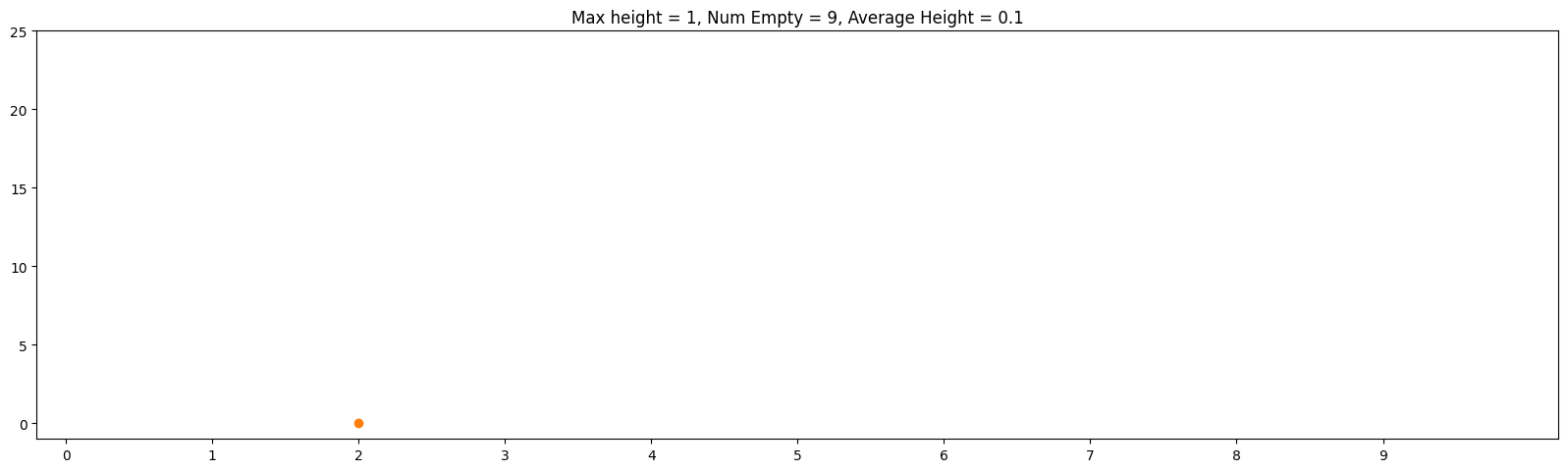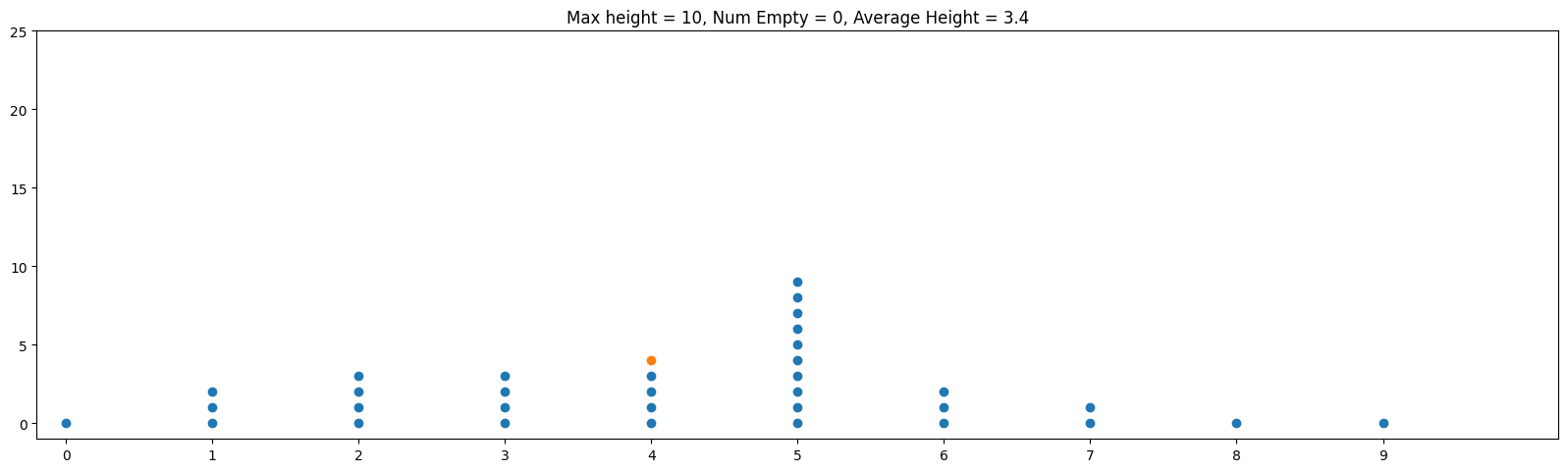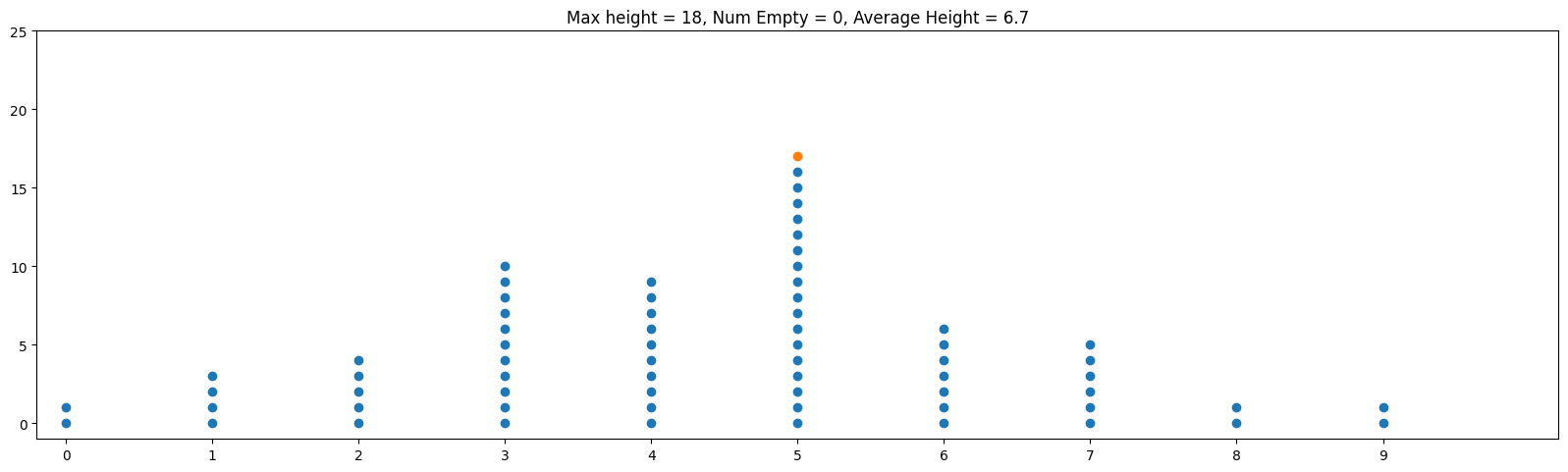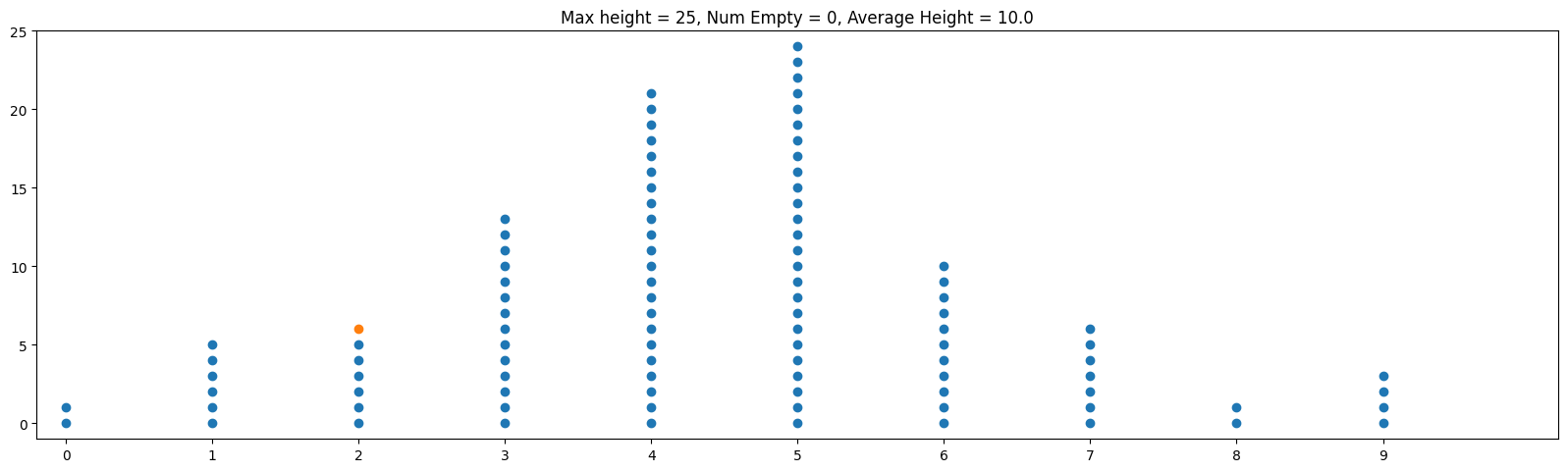
One thing that makes this a little less than ideal in practice is that the balls are skewed towards the center bins. By contrast, and ideal hash function is analogous to distributing the balls uniformly at random. This means that on any toss of a ball, we have an equal probability of 1/n of going into any particular bin. The animation below shows the same parameters m = 100, n = 100 but thrown uniformly at random

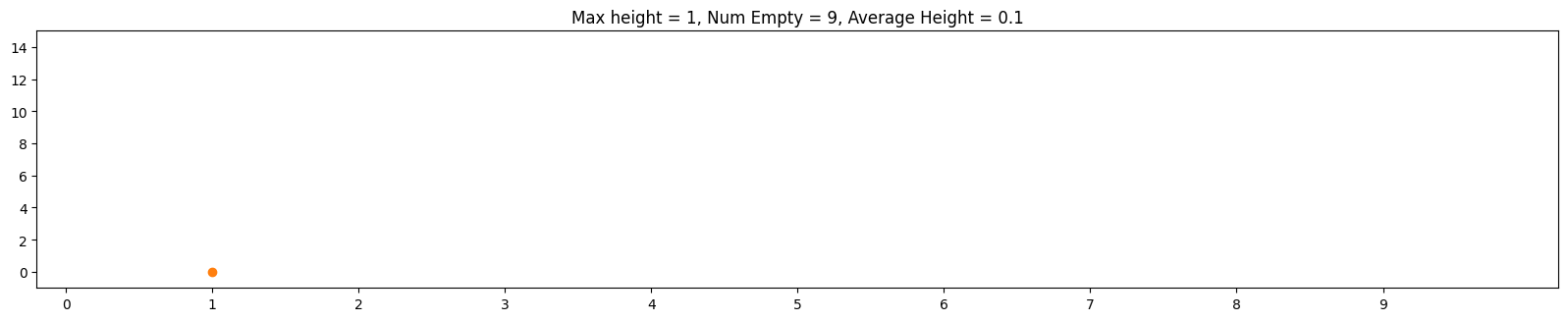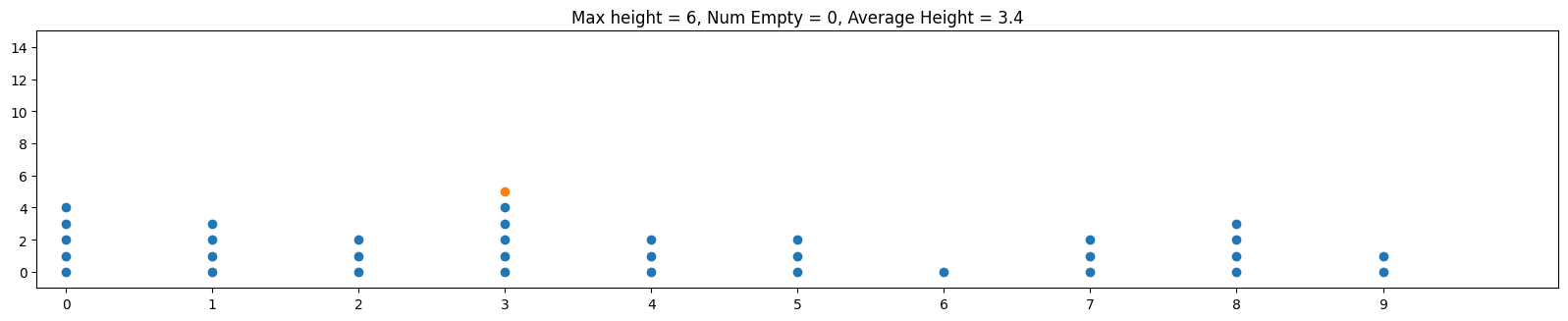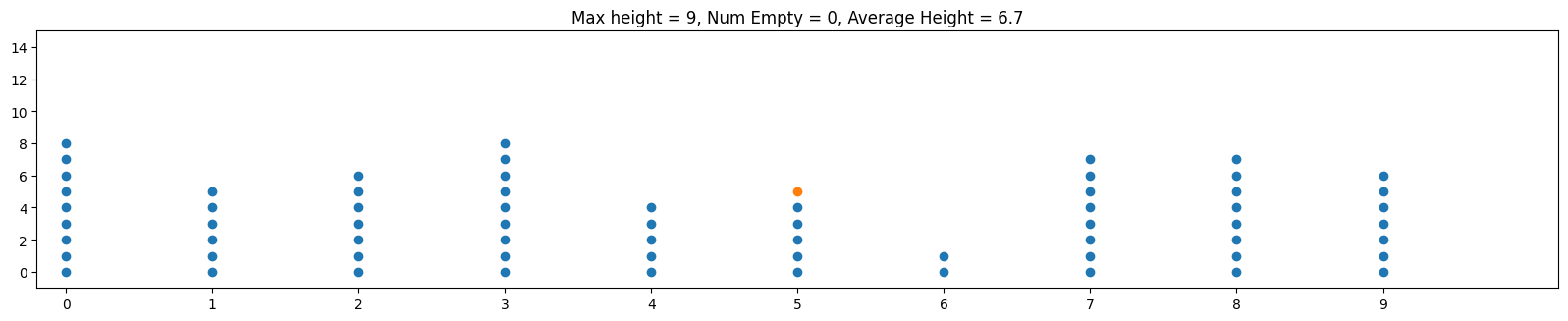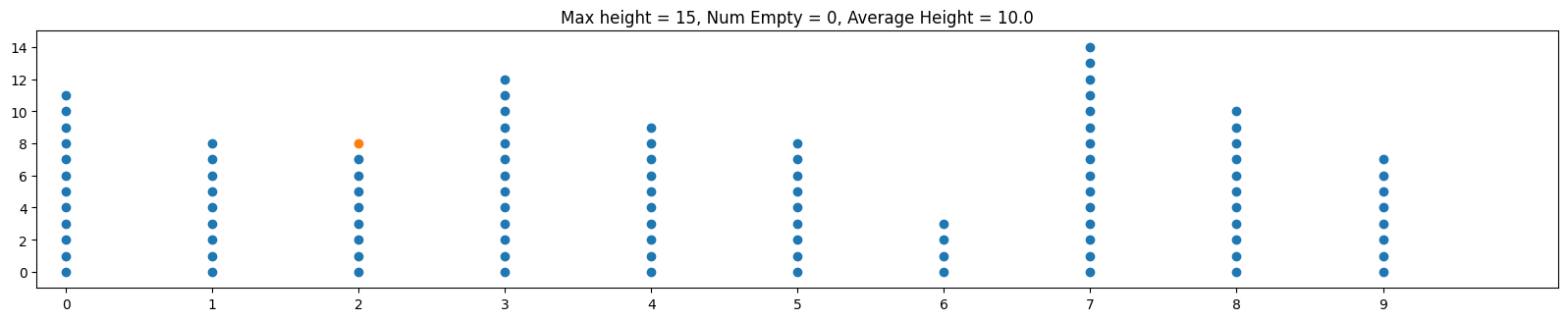
Notice how the balls are more evenly distributed. One implication is that the maximum height over all bins is smaller, so the worst case behavior is improved.

With this background, let's start to analyze the behavior

Exercise 1: Average Case Behavior

Given m objects in n bins, what is the average number of elements in any bin? Since it takes only constant time to jump to a bin, the dominant cost is walking through a linked list of a particular size, so this will give us an idea of the average time it takes to find an object.

Exercise 2: Worst Case Behavior

Click here to download the starter code for this exercise. You will be editing Experiments.py

Analyzing the worst case is more difficult analytically, but as always, let's do some experiments to try to make a hypothesis of what it is. Somehow, we hope to beat binary search, which is the best technique we've seen so far, but does that actually happen in practice? Let's do a couple of experiments

Experiment 1

For a fixed number of bins, vary the number of balls thrown into the bin and report the maximum number of balls in any bin after this. Some code has been provided to get you started in experiment_fixedbins. What would you posit the worst case time complexity is as a function of the number of balls m?

Experiment 2

Vary the number of bins n, and always throw m = n objects into the bins. This seems wasteful, as we have a bin for every object, but collisions are still possible (and probable) even here. What does the worst case here appear to be as a function of m=n?